- CRC (to detect the error in message and to discard it without correcting!).
For example, assume we have this code:
char data[]; // data to send
int n; // number of bytes
...
send(data, n);
...
receive(data, n);
...
after weaving, it looks like:
...
data[n]=CRC(data, n);
n:=n+1;
send(data, n);
...
receive(data, n);
if(data[n-1]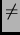 CRC(data, n-1)) ERROR();
CRC(data, n-1)) ERROR();
... - Triplication of the message sent (It also provides correction, satisfies property 1). It is
also time redundancy.
For example, after weaving:
...
send(data, n);
send(data, n);
send(data, n);
...
char mdata[3][];
receive(mdata[0], n);
receive(mdata[1], n);
receive(mdata[2], n);
data:=majority(mdata,3,n);
... - Sliding Window Protocol (Satisfies property 2).
- Triplicate SOME PART OF code on the same processor and apply majority voting on the output. i.e.
s1: exec(); (execution duration is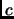 )
)
s2: save output[1]; (execution duration is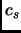 )
)
s3: exec();
s4: save output[2];
s5: exec();
s6: save output[3];
s7: output:= majority(output[i]);
Let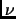 be the maximum duration of a failure and
be the maximum duration of a failure and 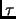 be
the interval between two consecutive failures.
For this scheme to work, we can write this assumption:
be
the interval between two consecutive failures.
For this scheme to work, we can write this assumption:
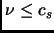 and
and 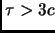 . If the transient failures are short but occurs
very frequently, then the code part to be triplicated should be reduced such that
. If the transient failures are short but occurs
very frequently, then the code part to be triplicated should be reduced such that
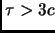 is satisfied, which increases the number of ``saving output'' phases,
and consequently the overhad.
is satisfied, which increases the number of ``saving output'' phases,
and consequently the overhad.
And also note that this helps immediate recovering from data flow errors, not control flow errors (for detection of control flow errors, signature monitoring can be used).
- Clock synchronization.
It may be needed for vaious fault-tolerant services.
we want that the clocks of any two processors are approximately equal at any time, i.e.
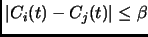 .
.
An approach for clk synchronization (Assumption is that all clocks are running at the same speed): At the beginning of each cycle (or perhaps more frequently?), monitor processor broadcasts its clock value (
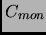 ) to all processors.
The travelling time of this message
is
) to all processors.
The travelling time of this message
is 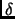 . So, it is delivered in
. So, it is delivered in
![$ [\delta-\epsilon, \delta+\epsilon]$](img23.png) .
.
Each processor makes this adjustment:
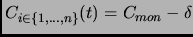 .
Moreover in heartbeat messages, all processors can send their clock values to
the monitor as feedback so that monitor can apply any control scheme to adjusts the clocks
better such that the monitor sends
.
Moreover in heartbeat messages, all processors can send their clock values to
the monitor as feedback so that monitor can apply any control scheme to adjusts the clocks
better such that the monitor sends
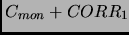 to processor 1,
to processor 1,
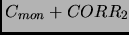 to processor 2
and so on.
to processor 2
and so on.
- Failure detection using heartbeating. Each processor sends heartbeats to
the monitor processor at a frequency in range of
![$ [\pi-\epsilon_p, \pi+\epsilon_p]$](img27.png) .
The travel time of the heartbeat is
.
The travel time of the heartbeat is
![$ [\delta-\epsilon_t, \delta+\epsilon_t]$](img28.png) .
The monitor runs a watchdog timer (
.
The monitor runs a watchdog timer (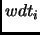 ) for each processor and if
) for each processor and if
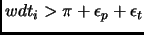 then it means that processor
then it means that processor 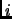 failed.
Note that the monitor can precisely define
failed.
Note that the monitor can precisely define
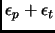 at run-time.
Therefore, the maximum time passed to detect a failure is
at run-time.
Therefore, the maximum time passed to detect a failure is
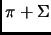 where
where 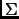 is
is
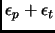 .
.
After the monitor receives all heartbeats at around time
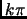 (i.e. it resets all watchdogs
related to processors), the monitor may send acknowledgments
(transmission time is
(i.e. it resets all watchdogs
related to processors), the monitor may send acknowledgments
(transmission time is
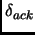 ). There are two kinds of ACKs:
Monitor can request a rollback to the previous state, or it just says okay, perhaps including
). There are two kinds of ACKs:
Monitor can request a rollback to the previous state, or it just says okay, perhaps including
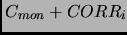 information for clock synchronization. Therefore, the recovery time after
failure occurs is
information for clock synchronization. Therefore, the recovery time after
failure occurs is
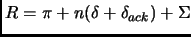 . This is the cost of recovery and our
real-time constraints should tolerate this.
. This is the cost of recovery and our
real-time constraints should tolerate this.
- Checkpointing and Rollback.
If we synchronize clocks, then we can use equidistant checkpointing. Each processor
checkpoints its local state by sending this state information to the
monitor processor at a frequency
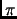 . So, checkpoints are taken at discrete times
. So, checkpoints are taken at discrete times
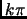 . Let
. Let 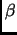 be the maximum clock difference between any
two processors, and
be the maximum clock difference between any
two processors, and 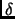 be the transmission time of message. For this scheme to work,
the assumption is
be the transmission time of message. For this scheme to work,
the assumption is
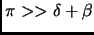 . On the other hand, there is a problem with
orphan and missing messages because of
. On the other hand, there is a problem with
orphan and missing messages because of 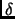 and
and 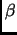 . We can solve this problem
as follows [Jal94]:
To prevent orphan messages, if there is a send() command within the interval
. We can solve this problem
as follows [Jal94]:
To prevent orphan messages, if there is a send() command within the interval
![$ [k\pi-\beta, k\pi]$](img41.png) , we must replace the checkpoint just before send(). To prevent
missing messages, message logging can be used. Sender logs the messages it sends
during interval
, we must replace the checkpoint just before send(). To prevent
missing messages, message logging can be used. Sender logs the messages it sends
during interval
![$ [k\pi-\delta-\beta,k\pi]$](img42.png) on a stable storage. If our assumption is that
there is not a stable storage on fail-silent processors and the only processor providing
fail-stop behavior is the monitor processor, then processors should insert these messages into
the hearbeat (or checkpointing) messages and send to the monitor (oops, overhead is getting bigger
and bigger!). If rollback is performed, then these messages are retransmitted after rollback. In a
similar way, receiver logs the messages in the critical interval
on a stable storage. If our assumption is that
there is not a stable storage on fail-silent processors and the only processor providing
fail-stop behavior is the monitor processor, then processors should insert these messages into
the hearbeat (or checkpointing) messages and send to the monitor (oops, overhead is getting bigger
and bigger!). If rollback is performed, then these messages are retransmitted after rollback. In a
similar way, receiver logs the messages in the critical interval
![$ [k\pi, k\pi+\delta+\beta]$](img43.png) too.
too.
- Atomic Actions.
Supporting atomicity is easy in uniprocessor systems; CP is taken at the beginning of the atomic action, if failure occurs before end system goes to the beginning of that action. In distributed systems, supporting atomic actions is more complicated because data can be accessed concurrently... (necessary for embedded systems?) - Data Resiliency by means of Replication.
If user enables data resiliency, the aspect will consider the replication of the specified data objects(e.g. primary site approach). When the primary site fails, one of the backup objects will be used. Another aspect that can be used as well is voting on the data objects. This aspect provides that performing an operation on replicated data is decided collectively by replicas through voting. Voting can mask both node a communication failures. (is data resiliency necessary for embedded systems?) - Process Resiliency by means of Replication.
If user enables task resiliency, the aspect will consider the replication of the specified tasks, and then there is no further need for rolling-back, when the replicated task fails (Primary site approach). For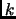 resilient task,
resilient task,
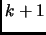 replication is necessary. If primary replica fails, one of the backup replicas
takes the place of the primary.
replication is necessary. If primary replica fails, one of the backup replicas
takes the place of the primary.