



|  |  | Formal semantics | Contents |
We give here the standard operational semantics of the "Simple" language.
They are summarized by the following table:
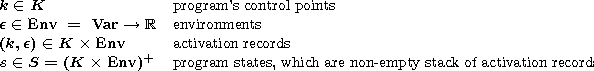
An environment is defined by a function assigning a value to a set of variables Var visible in the current scope. A program state is a non-empty stack of activation records. A stack is viewed as a word where the last letter corresponds to the top of the stack.
The semantics of a numerical expression nexpr is a function

We refer to [1] for the precise definition of this semantic function. The semantics of a Boolean expression bexpr is a function

which is defined inductively as follows:
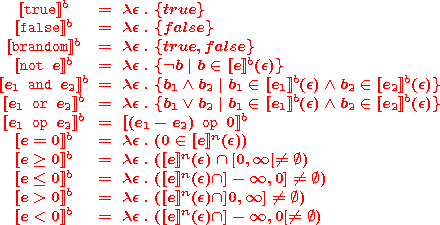
The semantics of a Boolean expression can be extended as a predicate on environments as follows:
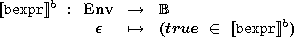
We define the semantics of a program as a discrete dynamical system (S,S0, -> ) where S is the state-space of the program (see above), S0 is the set of initial states, and -> is the transition relation between states. If k0 denotes the starting point of the main procedure, then S0 is defined as
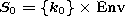
This reflects the hypothesis that variables are uninitialized (read: they may contain arbitrary values) at start. The transition relation is defined as follows:
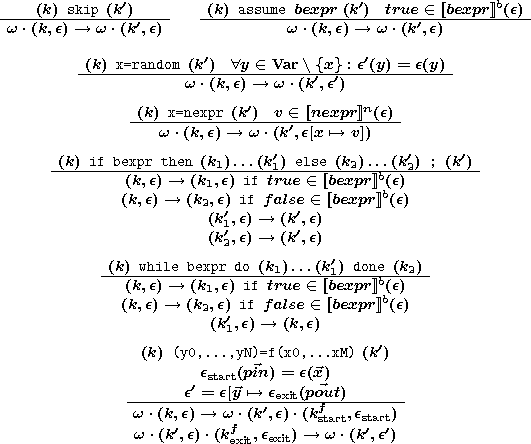

|  |  | Formal semantics | Contents |