TDs d'automates et applications
TD numéro 2

Table des matières

• Langage {aⁿ, n >= 0}
• Langage {aⁿbⁿ, n >= 0}
• Langage {aⁿbⁿcⁿ, n >= 0}
• Une preuve par induction

Trouver une grammaire G engendrant ce langage. Quel est son type (0, 1, 2 ou 3) ? Existe-t-il un automate d'états fini déterministe reconnaissant ce langage ? Si oui lequel ?

G = < {a}, {S}, S, R >
avec R: 
  S --> epsilon
  S --> a S

Cette grammaire est régulière, c'est-à-dire de type 3. En effet toutes les règles sont linéaires à droite. Le langage étant régulier, il existe un automate d'états fini déterministe qui le reconnaît. Le voici :

Trouver une grammaire G engendrant ce langage. Quel est son type (0, 1, 2 ou 3) ? Existe-t-il un automate d'états fini déterministe reconnaissant ce langage ? Si oui lequel ?

G = < {a,b}, {S}, S, R >
avec R: 
  S --> epsilon
  S --> a S b

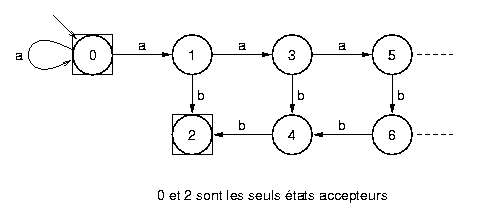
Cette grammaire est hors contexte, c'est-à-dire de type 2. En effet toutes les règles sont de la forme « A --> alpha », mais la seconde règle n'est pas linéaire. Il n'existe donc pas d'automate d'états fini déterministe reconnaissant ce langage. Par contre en voici un qui est infini :

Trouver une grammaire G engendrant ce langage. Quel est son type (0, 1, 2 ou 3) ? Existe-t-il un automate d'états fini déterministe reconnaissant ce langage ? Si oui lequel ?

G = < {a,b,c}, {S,B}, S, R >
avec R: 
  S  --> epsilon
  S  --> a S B c
  cB --> Bc
  aB --> ab
  bB --> bb

Cette grammaire n'est même pas sous contexte, c'est-à-dire de type 0. En effet la troisième règle « cB --> Bc » n'est pas de la forme « alpha B gamma --> alpha beta gamma » où alpha et gamma seraient dans V^*, beta serait dans V⁺, et B serait dans V_N. Il n'existe donc pas d'automate d'états fini déterministe reconnaissant ce langage. Attention, ceci ne signifie pas qu'il n'existe pas de grammaire sous contexte engendrant ce langage. C'est juste que je n'en n'ai pas trouvé !

Quel est le langage engendré par la grammaire suivante ?

G = < {a,b}, {S,A,B}, S, R >
avec R: 
  S --> aB        S --> bA
  A --> a         A --> aS        A --> bAA
  B --> b         B --> bS        B --> aBB

On peut remarquer tout d'abord que tous les mots engendrés sont de longueur paire. En fait le langage engendré L(G) est l'ensemble de tous les mots de V_T⁺ contenant le même nombre de a que de b.

On veut à présent démontrer ce résultat. On procède par induction sur la longueur des mots engendrés. Les hypothèses d'induction sont :

• H1.   S ==>^* w si et seulement si w contient autant de a que de b.

• H2.   A ==>^* w si et seulement si w contient un a de plus que de b.

• H3.   B ==>^* w si et seulement si w contient un b de plus que de a.

Pour chacune de ces trois hypothèses, on note P(w) la propriété à gauche du « si et seulement si », et Q(w) la propriété en partie droite. On commence par prouver que les trois équivalences H1, H2 et H3 sont vraies pour tout mot de longueur 1 ; puis on montre que si les trois équivalences sont vraies pour tout mot de longueur inférieure ou égale à n, alors elles sont également vraies pour tout mot de longueur inférieure ou égale à n+1.

• Il faut montrer que les trois hypothèses sont vraies pour tout mot w de longueur égale à 1.

  • Partie si. Il faut montrer que Q(w) implique P(w) pour tout mot w tel que lg(w) = 1.

    • H1. Il n'existe pas de mot w de longueur 1 contenant autant de a que de b, donc Q(w) = faux. De plus il n'existe pas de mot w de longueur 1 dérivable à partir de S, donc P(w) = faux. L'implication faux => faux étant vraie, H1 est vraie dans le sens « si ».

    • H2. Il existe un seul mot de longueur 1 contenant un a de plus que de b, c'est le mot « a » ; donc Q(w) = vrai. De plus il existe un seul mot de longueur 1 dérivable à partir de A, c'est le mot « a » ; donc P(w) = vrai. L'implication vrai => vrai étant vraie, H2 est vraie dans le sens « si ».

    • H3. Le même raisonnement que pour H2 permet de conclure que H3 est vraie dans le sens « si ».

  • Partie seulement si. Il faut montrer que P(w) implique Q(w) pour tout mot w tel que lg(w) = 1.

    • H1. Un raisonnement analogue à celui de la partie « si » de H1 permet de conclure que H1 est vraie dans le sens « seulement si ».

    • H2. Idem.

    • H3. Idem.

• Supposons que les trois hypothèses sont vraies pour tout mot de longueur inférieure ou égale à n. Il faut montrer qu'elles sont vraies pour tout mot de longueur inférieure ou égale à n+1.

  • Partie si. Il faut montrer que Q(w) implique P(w) pour tout mot w tel que lg(w) <= n+1.

    • H1. Le premier symbole de w est soit a soit b. Si c'est a, alors w = a.w' avec lg(w') <= n et w' contient un b de plus que de a. Par hypothèse d'induction, B ==>^* w'. Par conséquent S ==> aB ==>^* a.w' = w, c'est-à-dire S ==>^* w. Le cas où le premier symbole est un b est similaire. H1 est donc vraie dans le sens « si ».

    • H2. Le premier symbole de w est soit a soit b. Si c'est un a, alors w = a.w' avec lg(w') <= n et w' contient autant de a que de b. Par hypothèse d'induction, S ==>^* w'. Par conséquent A ==> aS ==>^* a.w' = w, c'est-à-dire A ==>^* w. H2 est donc vraie dans le sens « si ».

      Si le premier symbole de w est un b, alors w = b.w' avec lg(w') <= n et w' contient deux a de plus que de b. Donc on peut décomposer w' = w''.w''' tels que lg(w'') <= n, lg(w''') <= n et w'' et w''' contiennent autant de a que de b. Par hypothèse d'induction, S ==>^* w'' et S ==>^* w'''. Par conséquent A ==> bAA ==>^* b.w''.w''' = b.w' = w, c'est-à-dire A ==>^* w. H2 est donc vraie dans le sens « si ».

    • H3. Le même raisonnement que pour H2 permet de conclure que H3 est vraie dans le sens « si ».

  • Partie seulement si. Il faut montrer que P(w) implique Q(w) pour tout mot w tel que lg(w) <= n+1.

    • H1. Le premier symbole de w est soit a soit b. Si c'est a, alors w = a.w' avec lg(w') <= n et B ==>^* w'. Par hypothèse d'induction, w' contient un b de plus que de a. Par conséquent, w = a.w' contient autant de a que de b. Le cas où le premier symbole est un b est similaire. H1 est donc vraie dans le sens « seulement si ».

    • H2. Le premier symbole de w est soit a soit b. Si c'est un a, alors w = a.w' avec lg(w') <= n et S ==>^* w'. Par hypothèse d'induction, w' contient autant de a que de b. Par conséquent, w = a.w' contient un a de plus que de b.

      Si le premier symbole de w est un b, alors w = b.w'.w'' avec lg(w') <= n, A ==>^* w', lg(w'') <= n et A ==>^* w'. Par hypothèse d'induction, w' contient un a de plus que de b. Même chose pour w''. Par conséquent, w = a.w'.w'' contient un a de plus que de b. H2 est donc vraie dans le sens « seulement si ».

    • H3. Le même raisonnement que pour H2 permet de conclure que H3 est vraie dans le sens « seulement si ».