|
|---|
Trouver une grammaire G engendrant le langage construit sur le vocabulaire VT = {0,1} et tel que toute chaîne composée uniquement de 0 soit de longueur inférieure ou égale à 2. Quel est son type (0, 1, 2 ou 3) ? Quelle est l'expression régulière du langage ? Trouver un automate d'états fini avec epsilon-transitions engendrant ce langage. Trouver un automate d'états fini déterministe engendrant ce langage.
G1 = < {0,1}, {S}, S, R >
avec R:
S --> 1 S | 01 S | 001 S | 0 | 00 | epsilon
Cette grammaire est régulière, c'est-à-dire de type 3. En effet toutes les règles sont linéaires à droite. Pour trouver l'expression régulière du langage engendré, il faut résoudre le système suivant :
S = 1 S + 01 S + 001 S + 0 + 00 + epsilon
= (1 + 01 + 001) S + (0 + 00 + epsilon)
= (1 + 01 + 001)* . (0 + 00 + epsilon)
Toutefois cette grammaire est ambiguë. Par exemple, si le premier symbole est 0, on ne sait pas quelle règle de dérivation il faut appliquer. Il y a le choix entre 4 règles différentes. Une autre grammaire, non ambiguë celle-la, engendrant le même langage est :
G2 = < {0,1}, {S,A,B}, S, R >
avec R:
S --> 1 S | 0 A | epsilon
A --> 1 S | 0 B | epsilon
B --> 1 S | epsilon
Pour se convaincre que les deux grammaires G1 et G2 engendrent le même langages (elle ne sont pas identique), il suffit de chercher l'expression régulière du langage engendré par G2 :
S = 1 S + 0 A + epsilon A = 1 S + 0 B + epsilon B = 1 S + epsilon
D'où :
A = 1 S + 0 . (1 S + epsilon) + epsilon
= 1 S + 01 S + 0 + epsilon
S = 1 S + 0 . (1 S + 01 S + 0 + epsilon) + epsilon
= 1 S + 01 S + 001 S + 00 + 0 + epsilon
= (1 + 01 + 001) S + (00 + 0 + epsilon)
= (1 + 01 + 001)* . (00 + 0 + epsilon)
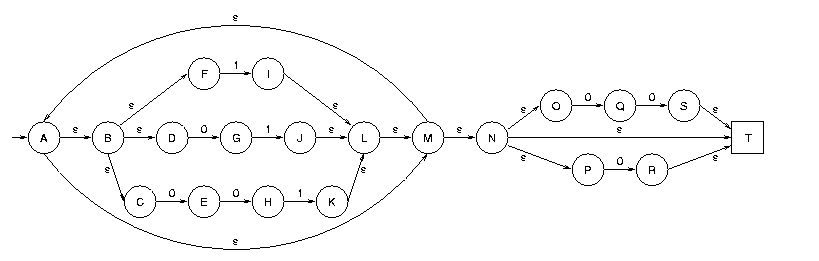
C'est bien la même expression régulière que celle obtenue pour G1. Voici l'automate avec epsilon-transitions construit à partir de cette expression régulière :

|
|---|
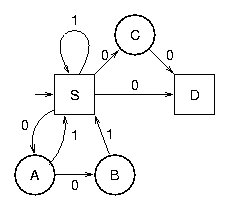
Cet automate contient des epsilon-transitions et n'est donc pas déterministe. Supprimer ses epsilon-transitions et le minimiser serait fastidieux vu sa taille. Il est par contre possible de trouver un automate d'états fini engendrant ce langage directement à partir de la grammaire. Avec la grammaire G1 on obtient :
|
|---|
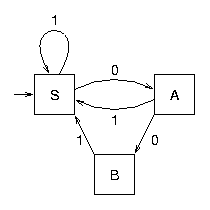
Cet automate non plus n'est pas déterministe. La raison est que la grammaire G1 est ambiguë. Au contraire, avec la grammaire G2 on obtient un automate d'états fini déterministe :
|
|---|
Si on avait essayé de déterminiser l'automate obtenu à partir de G1, on aurait obtenu exactement le même que celui obtenu à partir de G2. Les groupes d'états construits auraient été {S}, {A,C,D} et {B,D}. Comme ils contiennent tous un état terminal (S ou D), ces trois états sont terminaux.
Trouver l'expression régulière du langage construit sur le vocabulaire VT = {0,1} tel que tous les mots contiennent au moins un 1 et un 0. Trouver un automate d'états fini avec epsilon-transitions engendrant ce langage. Trouver un automate d'états fini déterministe engendrant ce langage.
Il y a deux approches. La première consiste à considérer que tout mot contient nécessairement la chaîne « 01 » ou la chaîne « 10 », avec avant et après n'importe quelle succession de 0 et de 1. Cela donne :
E1 = (0 + 1)*.(01 + 10).(0 + 1)*
La seconde approche consiste à considérer que tout mot commence soit par 1 soit par 0. Supposons que le mot commence par 1. On sait qu'il contient aussi au moins un 0 après ce 1. Le premier 0 qu'il contient existe et est par conséquent précédé uniquement de 1. Après ce premier 0, on a une succession quelconque de 0 et de 1. Le raisonnement est symmétrique si le mot commence par 0. Cela donne :
E2 = (0.0*.1 + 1.1*.0).(0 + 1)*
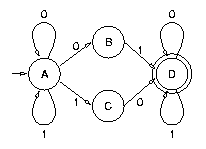
Voici l'automate d'états fini construit à partir de E1. Il n'est pas déterministe :
|
|---|
Et voici l'automate d'états fini construit à partir de E2. Il est déterministe :
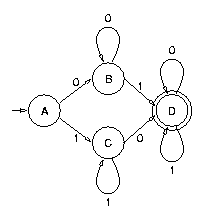
|
|---|