|
|---|
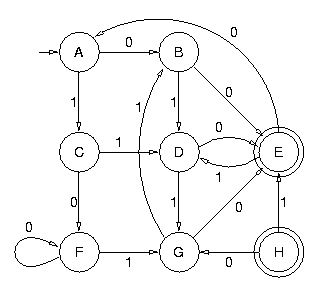
Minimiser l'automate fini suivant :

|
|---|
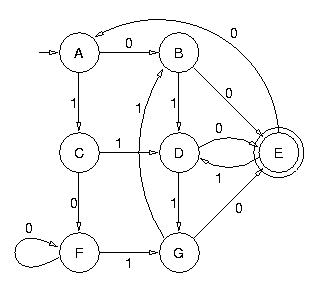
On commence par rendre cet automate initialement connecté. On supprime donc l'état H qui n'est pas accessible. On supprime du même coup les deux transitions de H vers E et de H vers G :
|
|---|
Puis on calcule les classes d'états équivalents pour la relation d'équivalence induite par l'automate. On partitionne donc incrémentalement l'ensemble des états de l'automate, en commençant par la partition états finals/états non finals. À partir de cette première partition, on construit les autres partitions jusqu'à obtenir un point fixe :
{A,B,C,D,F,G} {E}
{A,C,F} {B,D,G} {E}
{A} {C,F} {B,D,G} {E}
{A} {C,F} {B,D,G} {E}
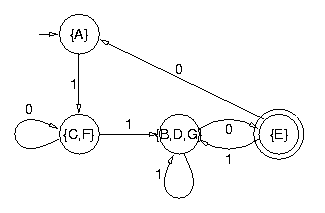
L'automate minimal équivalent est donc :
|
|---|
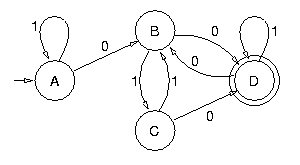
Minimiser l'automate fini suivant :
|
|---|
La première étape consiste à inverser les flèches. Ce faisant, l'état initial devient final et les états finals deviennent initiaux :
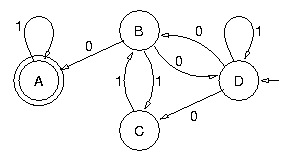
|
|---|
L'automate ainsi obtenu n'est pas déterministe. La deuxième étape consiste à le déterminiser, ce qui donne :
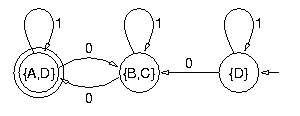
|
|---|
La troisième étape consiste à inverser à nouveau les flèches. Auparavant on a renommé les états par soucis de lisibilité :
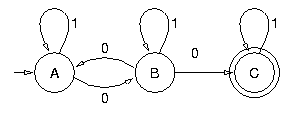
|
|---|
La quatrième et dernière étape consiste à déterminiser cet automate. On obtient ainsi l'automate minimal équivalent à l'automate initial :
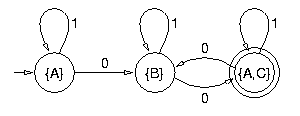
|
|---|
Trouver l'expression régulière du langage reconnu par l'automate fini déterministe suivant :

|
|---|
On commence par calculer le système régulier correspondant à cet automate :
A = 0A + 1B + epsilon B = 0C + 1B C = 0A + 1B
Selon la façon dont on résout ce système, c'est-à-dire l'ordre dans lequel on effectue les substitutions, on trouve deux expressions régulières différentes :
e1 = (0 + 1.(1 + 01)*.00)* e2 = (0 + 1.(1 + 0.(10)*.11)*.0.(10)*.0)*
Ces deux expressions régulières, bien que différentes, représentent le même langage régulier.
La deuxième question est de calculer l'expression régulière du langage reconnu par l'automate mais en en passant pas plus d'une fois par l'état B. Il faut donc modifier le système régulier pour tenir compte de cette contrainte, puis résoudre le système modifié :
A = 0A + 1B + epsilon B = 0C C = 0A' A' = 0A' + epsilon
La résolution donne l'expression régulière suivante :
e = 0*.(epsilon + 100.0*)